Edit on GitHub

MultiscaleGraphSignalTransforms.jl

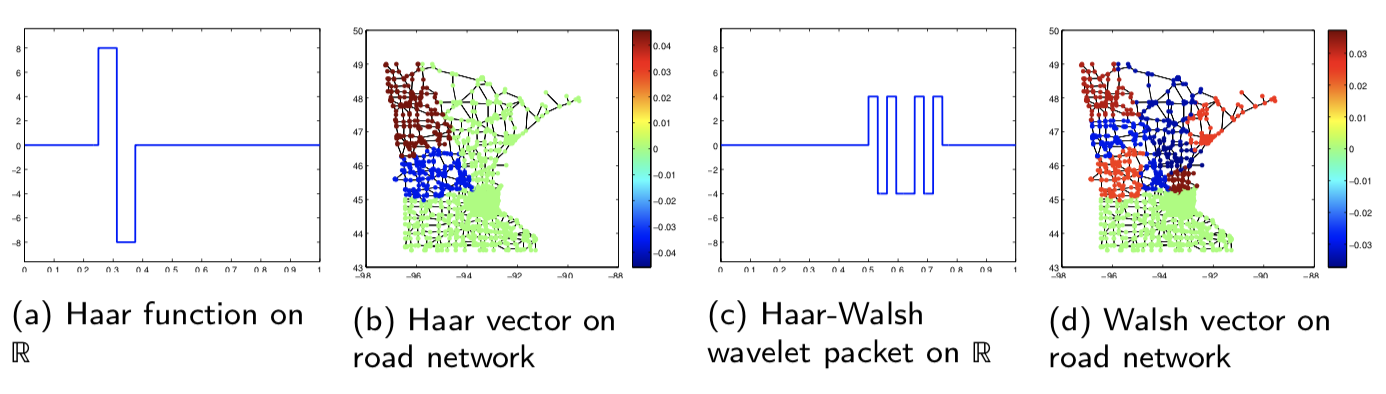
Haar-Walsh on R vs on Graph

MultiscaleGraphSignalTransforms.jl is a collection of tools for graph signal processing including HGLET, GHWT, eGHWT, NGWP, Lapped NGWP, and Lapped HGLET. Some of them were originally written in MATLAB by Jeff Irion, but we added more functionalities, e.g., eGHWT, NGWP, etc.

Copyright 2015-2021 The Regents of the University of California

Implemented by Jeff Irion, Haotian Li, Naoki Saito, and Yiqun Shao

SETUP

To install the MultiscaleGraphSignalTransforms.jl, run

julia> import Pkg; Pkg.add("MultiscaleGraphSignalTransforms")
julia> using MultiscaleGraphSignalTransforms

GETTING STARTED

Currently, you can run a set of very small tests via ] test MultiscaleGraphSignalTransforms; see the actual file test/runtest.jl for more details.

You can also check out the examples we provided in the sidebar.

REFERENCES

  1. J. Irion and N. Saito, Hierarchical graph Laplacian eigen transforms, Japan SIAM Letters, vol. 6, pp. 21-24, 2014.
  2. J. Irion and N. Saito, The generalized Haar-Walsh transform, Proc. 2014 IEEE Statistical Signal Processing Workshop, pp. 488-491, 2014.
  3. J. Irion and N. Saito, Applied and computational harmonic analysis on graphs and networks, Wavelets and Sparsity XVI, (M. Papadakis, V. K. Goyal, D. Van De Ville, eds.), Proc. SPIE 9597, Paper #95971F, Invited paper, 2015.
  4. J. Irion, Multiscale Transforms for Signals on Graphs: Methods and Applications, Ph.D. dissertation, University of California, Davis, Dec. 2015.
  5. J. Irion and N. Saito, Learning sparsity and structure of matrices with multiscale graph basis dictionaries, Proc. 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP), (A. Uncini, K. Diamantaras, F. A. N. Palmieri, and J. Larsen, eds.), 2016.
  6. J. Irion and N. Saito, Efficient approximation and denoising of graph signals using the multiscale basis dictionaries, IEEE Transactions on Signal and Information Processing over Networks, Vol. 3, no. 3, pp. 607-616, 2017.
  7. Y. Shao and N. Saito, The extended Generalized Haar-Walsh Transform and applications, Wavelets and Sparsity XVIII, (D. Van De Ville, M. Papadakis, and Y. M. Lu, eds.), Proc. SPIE 11138, Paper #111380C, 2019.
  8. Y. Shao, The Extended Generalized Haar-Walsh Transform and Applications, Ph.D. dissertation, University of California, Davis, Sep. 2020.
  9. H. Li and N. Saito, Metrics of graph Laplacian eigenvectors, Wavelets and Sparsity XVIII, (D. Van De Ville, M. Papadakis, and Y. M. Lu, eds.), Proc. SPIE 11138, Paper #111381K, 2019.
  10. C. Alexander, H. Li and N. Saito, Natural graph wavelet packet dictionaries, J. Fourier Anal. Appl., vol. 27, Article #41, 2021.
  11. H. Li, Natural Graph Wavelet Dictionaries: Methods and Applications, Ph.D. dissertation, University of California, Davis, Jun. 2021.